来源:站酷 作者:阿摩那

四方连续以对称为主要特色。“对称”这一概念远比字面意思要丰富得多，有大量变种。美国宾夕法尼亚的考古学家Dorothy K. WashBurn研究了各种古代文化经典图案中的对称规律，和威斯康辛大学的数学教授Donald W. Crowe合作写了一本洋洋大观的专著《对称的文化》，中译本为《设计.对称性设计教程与解析》，可见其内涵之丰富。

我们这个插件只用了4种对称方式，以后有时间再慢慢添加更多。

下载地址：共享插件002】四方连续.rar

CorelDraw X3以上版本适用。测试过X3和X6，其他版本使用出现问题请及时反馈。

照例简单说明一下使用方法，如果您已经用过雪花插件，这节灰色的字体可以跳过。

<使用说明>

这个插件内嵌在一个cdr文档中，避免了用户安装插件的麻烦，只要打开这个名为“【共享插件002】四方连续.cdr”的文档，就可以立即使用了。

由于插件以宏的形式运行，打开时会跳出病毒警告：

选择“启用宏”，代码是安全的。

如果没有跳出上述警告，说明宏被自动屏蔽了，需要调整一下安全级别。

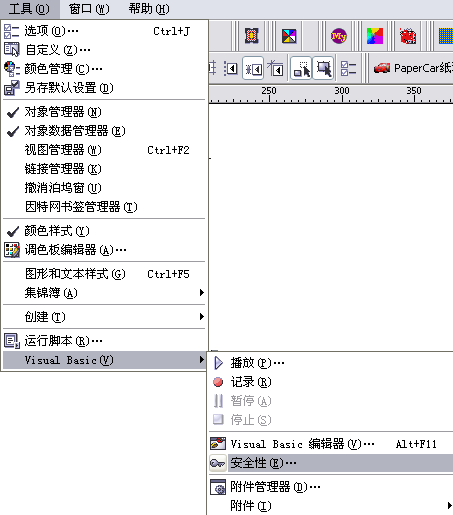
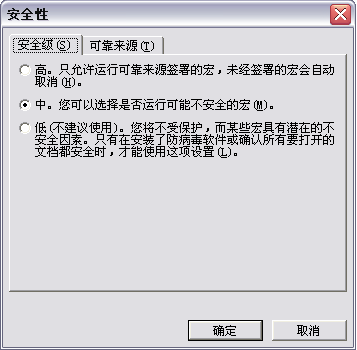
安全级别设置为“中”，这也是默认设置。

首先跳出来的是用户界面：

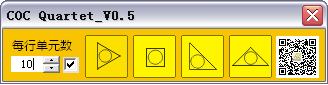
以及做好的一个图案样例，也就是本文的题图了。

我们仍然相信一个合理的界面设计不需要说明书。况且，貌似也没有很多选项让用户去瞎折腾。

中间四个按钮干正事，最右边的按钮打广告，敬请关注“创意之代码”：

这个插件要求用户选择一个或几个物体作为单元，然后按中间四个按钮所示的方式进行阵列与镜像，形成连续图案。注意，不能选择位图作为单元。不是做不到，而是作者觉得没这个必要，阵列一大批位图会让计算机速度变得很慢。如果真有人需要用位图做单元，请及时告知，我们专为你开发。

“每行单元数”是指图案的每行排列多少个单元，这个数字表达的含义根据图案生成方式的不同有所差异。

那个小小的复选项选中后，会对最后生成的图案做一个简单的渐变配色加黑背景，如本文题图。去掉这个复选项，则最后的图案保持单元色彩，背景为白色。

文档中有若干个页面，前两个页面是插件生成的图案样例，第三个页面是19个古典图案符号，供用户测试插件（效果还不错）。其他页面都是本文出现过的测试结果图。

以第一个按钮为例，我们看看它能把一个简单的方块变成什么。

一个方块，简单得不能再简单了：

第一个按钮把它变成了这样：

第三个按钮把它变成了这样：

第四个按钮把它变成了这样：

一个随手画出来的三角形，第一个按钮把它变成这样：

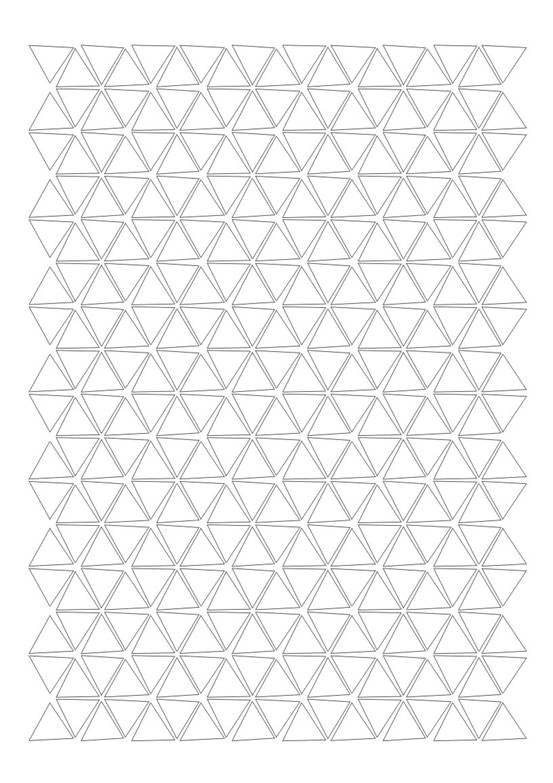
三角形转了一个角度后，效果变化有点大（还是第一个按钮）：

第二个按钮的效果比较传统，但也不算难看：

第三个按钮把它变成这样：

第四个按钮把它变成这样：

哪怕是一坨便便：

也能把它打扮得像富丽堂皇！

插件里的填色模块可以识别单元是封闭图形还是开放的曲线。如是前者，就填色，边线设为无；如是后者，就渲染边线，比如便便图。边线粗细用户自行设置，反正也简单，插件就不代劳了。

这个四方连续插件的编写过程比想象的要复杂，虽然原理很简单。

要处理的主要问题是纹样形成后不能留下太多空隙，造成图案疏松影响了四方连续的古典繁复之美。插件的4种连续图案生成方式均不产生单元间的重叠，除非所选的单元内部本身就带有重叠。

既不留空隙，又不重叠，实际上需要的就是一个与单元贴边的包围盒了。只是除第二个外，其他三个包围盒都不是正方的。

带有斜边的包围盒需要计算斜边与图形的最外切点，因此必须以一定的密度遍历图形中的点。上面这个三角形包围盒在最外切点基础上稍微往外扩了一圈，给图形的线宽设置留下一定裕量，以免增加线宽后产生邻接重叠。

四种连续方式的包围盒显示出来是这样的：

最下面的三角形框，它要重复到第6个单元才算完成一个周期。下数第二行周期是4，第三行周期是8，最上面一行周期是2。图案通常在纵向也有周期，一般是2。

单元的选择不会正好填满一个包围盒，因此最后做出来的四方连续图案还是有不少空隙。这些空隙可以使用一种“匹配”的方式来填充，让图案看起来有生动感，而不像是一块块雕花板砖的机械拼接。别忘了，这种图案的名称是“连续”。这项功能以后改版更新时再添加。

最后这个图案保持了单元的原始色彩（去除了复选框的默认选中状态）：

单元：

本插件的开发从一开始就贯彻了“包围盒”的概念，从这个概念出发，可以发现四方连续图案的设计其实可以划归为平面空间分割的研究，那是一个非常有意思的数学分支。Escher的大部分作品都在利用平面空间分割规律，只是他很巧妙地的把精心设计的变化多端的包围盒从观众的视线中隐藏了起来。

插件动手开发时，本以为找到了一类设计规律的通解，开发完成后才发现那不过是一个更抽象、更高层的设计规律的特解之一（实例）。

从平面分割的角度，连续图案甚至可以是非周期性的，如Penrose准晶体图案，但其魅力依旧。

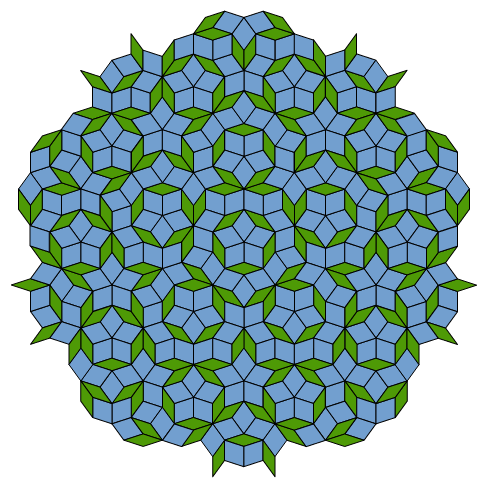
晚安。

更多神器:设计师神器大集合